【推薦】賭王何鴻燊永遠不會輸,5000億財富背後的終極秘密:凱利公式
摘要:賭徒迷信的是運氣,何鴻燊相信的是數學。
賭徒迷信的是運氣,
何鴻燊相信的是數學。
一、賭王何鴻燊
2020年5月26日,賭王何鴻燊逝世,享年98歲。
這一天中午,港澳地區突降大雨。
這位知名的港澳企業家,素有“澳門賭王”之稱的傳奇人物,至此謝幕。
1961年,澳葡政府規定博彩業須通過專營制度實施。
何鴻燊看準時機,接手葡京賭場,從此事業蒸蒸日上。
直至今日,何鴻燊及其家族控制著高達5000億港元的資產。

何鴻燊
曾有人請教何鴻燊:“如果他們老是贏怎麼辦?”
老爺子說過一句名言:“不怕你贏,就怕你不來。”
在何鴻燊的眼中,他是不可能輸的。
因為他賭的不是運氣,而是數學。
一個現代的賭場,它集中了概率學、統計學等諸多知識。
所謂的各種致勝絕技,除了《賭聖》裏的周星馳,現實世界裏的周潤發都不信。
一個癡迷於發財夢的賭徒永遠不明白,與自己對賭的不是運氣,也不是莊家,而是狄利克雷、伯努利、高斯、納什、凱利這樣的數學大 師,贏的概率能有多大?
二、看得到的是概率看不見的是陷阱
何鴻燊的記憶力和算力一直堪稱神奇,
他創業期間,澳門的兩千多個電話號碼,他能倒背如流。
直接比複雜的賭 博遊戲,在數學上可能比不過。
就來一個最簡單的玩法:與何鴻燊比拋硬幣。
規則是這樣的:
擲硬幣,正面贏反面輸,如果你贏了可以拿走比賭注多一倍的錢,如果輸了則會賠掉本金。
你一聽可能覺得這遊戲還不錯,公平!
於是你拿出了身上的100元來玩這個遊戲,每次下注5元,這樣你至少有20次的下注機會。
不過,你運氣不太好,第一把就是反面,輸了5塊錢。
生性樂觀的你覺得沒什麼,反正不管怎麼說,贏面都有50%,下一把就可以贏回來。
結果,很快你就把身上的錢都輸光了。

你百思不得其解,明明是公平的50%贏面,在50%概率下至少不會虧本的,可為什麼最後會輸光?
事實上,你以為自己看到了50%的概率,把遊戲看得透徹明白,殊不知,你看到了概率,卻沒有看到背後的陷阱:大數定律。
三、大數定律
你覺得遊戲是公平的:
一正一反,均為50%概率,按照大數定律來說,這是必然規律。
然而,你有沒有想過,正是這種你以為的“公平”,讓你誤解了大數定律,才陷入了“賭徒謬論”裏呢?
先來看看這種讓你覺得“公平”的大數定律究竟是什麼。
它是數學家伯努利提出的:
假設n是N次獨 立重複試驗中事件A發生的次數,p是每一次試驗中A發生的概率,那麼,當N趨於無窮時:

式中n表示發生次數,N表示試驗總次數。
也就是說,大量重複的隨機現象裏其實藏著某種必然規律。
還是以擲硬幣為例,當投擲次數足夠大時,出現正(反)面的頻率將逐漸接近於1/2,且隨著投擲次數的增加,偏差會越來越小,如下圖。這是最早發現的大數定律之一。

擲硬幣頻率分佈圖
從表面概率看,這確實是場公平的遊戲。
但這種公平是有一定條件的,注意,這就是普通人看不到的。
大數定律講究“大量重複的隨機現象”,只有足夠多次試驗才能使得硬幣正反面出現次數與總次數之比幾乎等於1/2。
可具體多少次才算“足夠多”?才能夠把它用在個人對賭上?
沒有人知道。因為,概率論給出的答案是——無窮大。誰也不知道無窮大有多大,只知道這是一個令人仰望的數量。
可投擲硬幣次數越小,大數定律的身影就越模糊,可能10次中5正5反,也可能9正1反,也可能10正0反或0正10反……
現實往往是,在遠未達到“足夠多”次試驗時,你就已經輸了個精光了。
你覺得自己比何鴻燊更有錢嗎?
你身上有100元結果如此,你身上有10000元結果也是如此,就算你身上有一百萬也是如此,因為你永遠不可能有“足夠多”。
“輸贏概率為50%”,這本身就具有很大的誤導性。在硬幣拋出之前,50%的概率代表的是可能性;在硬幣拋出之後,50%代表的是結果的統計平均值,卻並不是實際分佈值。
這是你對大數定律的誤解之一。
把“大數定律”當“小數定律”,覺得遊戲是無條件“公平”的,正面和反面出現的頻率都為1/2。
這種在潛意識裏被奉為圭臬的“公平”,緊接著讓你踏入了第二個誤解——“賭徒謬論”。
四、賭徒謬論
大數定律有一個明顯的潛臺詞:
當隨機事件發生的次數足夠多時,發生的頻率便趨近於預期的概率。但人們常常錯誤地理解為:隨機意味著均勻。
如果過去一段時間內發生的事件不均勻,大家就會“人工”地從心理上把未來的事情“抹平”。也就是,如果輸了第一把,那下一把的贏面就會更大。
這種你下一把就可以贏回來的強烈錯覺,就是“賭徒謬論”。

當你玩遊戲連輸時,你的心底突然冒出一個神秘的聲音,它激動地朝你呐喊:穩住,風水輪流轉,下一把你很有可能就要贏了何鴻燊!
而其實,上一把和下一把之間並沒有任何聯繫。
就好比一個笑話:
在乘坐飛機時帶著一枚炸彈就不會遇上恐怖 分子了,因為同一架飛機上有兩枚炸彈的可能性是極小的。
兩者如出一轍,都把獨 立事件誤認為是互相關聯的事件。
要知道,大數定律的工作機制,可不是為了平衡對抗。
在這場遊戲中,任意兩次事件之間並不會相互產生影響。
賭局是沒有記憶的,哪怕你曾經輸了多次,它也不會因此給你更多勝出的機會。
五、只要進了賭場你就是一個窮鬼
你不服,想與何鴻燊再來一把。
遊戲仍然很簡單:還是拋硬幣。
何鴻燊沒有別的要求,這次你要來他的賭場賭。
規則還和前面一樣:擲硬幣,正面贏反面輸,如果你贏了可以贏走比賭注多一倍的錢,如果輸了則會賠掉本金。

這一次你運氣很不錯,第一把你就贏了何鴻燊100元!可把你高興壞了!
但是和前面的個人對賭相比,這次多了一個賭場。
賭場跟你說:“你看你也贏了這麼多,我呢,辛辛苦苦搭個場子,最後什麼都沒撈著。要不這樣,你贏了,就給我留下2%當流水,就算是救濟救濟老哥,給捧捧場!”
你想了下,2%也不多,拿去吧,不差錢!好了,這事就這麼定下來了。
然而你做夢都想不到的是:就是這小小的2%,又一次讓你輸得傾家蕩產!
你同樣百思不得其解,不過是小小的2%抽水,毫不起眼,明明也是開門紅,玩了很多把,贏了不少,可為什麼在最後,它就成為了莊家賺錢的利器,自己又輸光了?
天真的你,肯定不知道在賭場有一個逃不開的魔咒:賭徒破產困境。
六、賭徒破產困境
一鼓作氣,鴻運當頭。
第1把,贏;第2把,贏;第3把……
你覺得自己被幸運女神眷顧,一身富貴命。
可早在18世紀初,那群熱愛賭 博的概率論數學家們,就提出了那個讓賭徒聞風喪膽的破產噩夢:
在“公平”的賭 博中,任何一個擁有有限賭本的賭徒,只要長期賭下去,必然有一天會輸個精光。
我們來看看,為什麼那麼多長期賭徒都輸成了窮光蛋?錢都到哪去了?
假如你的小金庫是r,你帶著小金庫和莊家開始了一場追逐多巴胺刺 激的賭 博遊戲,打算贏得s後就離開,每一局你贏得籌碼的概率為p,那你輸光小金庫的概率有多大呢?
我們可以在馬爾科夫鏈、二項分佈、遞推公式等的助攻下,列出一組組粗暴的、令人頭皮發麻的函數,但也許它們都不如一張二維模擬圖來得直白,如下圖所示。

賭徒破產定理模擬圖
把不同r對應的f(r,n)和f(r,s,p)放到同一個圖中進行比較,它形象地揭示了賭徒輸光定理的含義:所謂的“公平”賭 博,其實並不公平。
在f(r,n)中,隨著次數n的增加,賭徒輸光的概率會逐漸增加並趨近於1,並且r越小,這種趨勢越明顯。這說明在公平賭 博的情況下,擁有籌碼更少的賭徒會更容易破產。
而在f(r,s,p)中,右側的圖則以一種冷峻而無情的話語告訴我們:如果希望輸光的概率比較小,那麼需要每次的贏面p足夠大或者是手裏的籌碼r足夠多。
你真能從莊家那裏虎口奪食、在贏面和籌碼中PK一把嗎?
答案,顯然是難乎其難的。
第一,莊家不是賭徒。
莊家的背後是賭場,也就意味著莊家相比於你,擁有“無限財富”。你的小金庫永遠比不過莊家的賭場錢莊,這也意味著,你比莊家更容易山窮水盡。
當然,也許你家裏有礦,壕到一擲千金,壕到家產超過5000億。
但超級賭場也會設置最大投注額,這並不是他們好心,想保護你免遭破產,他們只是為了自保才設計了一道安全屏障,來抵抗“無限財富”帶來的破產威脅。畢竟萬一哪天比爾蓋茨去賭場找樂子,一次性砸個幾百億進去,那賭場老闆恐怕真的要哭了。
第二,莊家是“抽水”收入。
忘了拋幣遊戲中那毫不起眼的2%了嗎?賭徒贏錢後,莊家會從賭徒手中抽取一定比例的流水傭金。
這樣一來,即使你有一個小金庫足以和莊家慢慢磨,打一場持久戰,但贏得越多,為莊家送去的“抽水”越多。長此以往,你還是輸了,錢都進了莊家的口袋。
最終,莊家賺的錢只跟賭徒下注大小有關。
你還是難以逃開那個牢籠般的魔咒,一步一步,走向了兩袖清風、空空如也的境地。
這世上,天才終究是少數,而“賭神”、“賭王”之所以成為普通賭徒難以望其項背的存在,不僅因為他們深諳賭徒心理,也不僅因為他們懂賭場規則,更因為他們懂得該下注多少。
七、賭王的眼中只有“窮鬼”
在賭王何鴻燊的眼裏,世界上或許只有兩種人:
一種現在是窮鬼,一種未來是窮鬼。
但有時賭場老闆也會有所忌憚,特別是遇到善用數學博弈的高手之時。
其中,凱利公式在高級賭徒的世界裏大名鼎鼎,是頂級高手常用的數學利器。
它也是賭場老闆最擔心被暴露的賭場秘密。
那什麼是凱利公式,我們先看一個例子:
一個1賠2(不包括本金)的簡單賭局,扔硬幣下注,假設賭注為1元,硬幣如果為正面則淨贏2元,如果為反面則輸掉1元。現在你的總資產為100元,每一次的押注都可投入任意金額。
你會怎麼賭呢?已知擲硬幣後正反面的概率都為50%,賠率是1賠2(不包括本金),那麼這個賭局其實只要耐心不斷地去下注,再拋開不公平因素的干擾,幾乎就能賺。

因為擲硬幣次數越多,其正反面出現概率就越會穩定在50%,收益2倍,損失卻只是1倍,從數學上講那是穩賺不賠的賭局。
但實際情況卻可能會有偏差。
如果你是冒險主義者
你可能會想,要玩就玩票大的,All In!一次性把100元全押上,幸運的話,一次正面就可以獲得200元,又是一段值得炫耀的賭史。
可是,如果輸了,得把100元資產拱手獻給對方,你就一無所有。好不容易來趟拉斯維加斯,這肯定不是明策。
如果你是保守主義者
你可能會想,謹慎點,百分之一慢慢來。
你每次只下注1元,正面贏2元,反面輸1元。
玩了20把突然覺得,對方下注10元一次就贏得20元,自己1次才贏2元、10次才能贏得20元,感覺自己已經錯過幾個億而開始後悔!
那到底該以多少比例下注才能獲得最大收益呢?
普通賭徒一般一臉茫然,但凱利公式卻能夠告訴我們答案:
計算後每次下注比例為當時總資金的25%,這樣就能獲得最大收益。
八、賭場大BOSS:凱利公式
讓我們來看看凱利公式的廬山真面目:
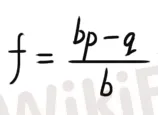
在公式中,各參數意義為:
f = 應投注的資本比例;
p = 獲勝的概率(也就是拋硬幣正面的概率);
q = 失敗的概率,即(1 - p)(也就是硬幣反面的概率);
b = 賠率,等於期望盈利 ÷可能虧損(也就是盈虧比);
公式上面的分子(bp-q)代表“贏面”,數學中叫“期望值”。
什麼才是不多不少的合適賭注呢?凱利告訴我們要通過選擇最佳投注比例,才能長期獲得最高盈利。
回到前面提到的例子中,硬幣拋出正反面的概率都是50%,所以p、q獲勝失敗的概率都為0.5,而賠率=期望盈利÷可能虧損=2元盈利÷1元虧損,賠率就是2,我們要求的答案是f,也就是(bp - q) ÷ b = (2 * 50% - 50%) ÷ 2 = 25%。
由此,我們根據凱利公式的計算而得投注比例,每次都拿出當前手中資金的25%來進行下注。設初始資金為100,硬幣為正面時收益為投注的2倍,為反面則失去投注金額。在下表中,我們模擬計算了10次賭局的收益情況。

表1-25%投注下10次收益表

表2-25%投注下10次收益表
表1從先正後反的情況計算了收益,而表2則計算了正反分佈交錯情況下的收益結果。
比較兩表,我們最終可以發現其收益是相等的,硬幣出現正反面的先後順序對於最終收益的計算結果並無影響。
而按25%的投注比例進行投注,收益基本呈現穩步增長的大趨勢。
但假設投注比例為100%時,10次當中只要出現任意一次的反面,就會徹底輸光身上的所有錢,直接出局,且每輪反面概率還為50%;
而每次1元1元地投注,也就是投注比例為1%的時候,10次數學上的收益為100+10×50%×2+(-1)×10×50%=105,這風險很小,不過收益太低。由此看來,凱利公式才是最大的贏家。
賭場操盤者每一次下注的時候,都會謹記數學原則;而作為普通賭徒,除了心中默念“菩薩保佑”外,哪里知道這後面的數學知識。
所以,就算你贏得了財神爺的支持,但你也永遠贏不了“凱利公式”。
九、除非100%贏否則任何時候都不應下注
所有的賭場遊戲,幾乎都是對賭徒不公平的遊戲。
但這種不公平並非是莊家出老千,現代賭場光明正大地依靠數學規則賺取利潤,從某種意義上來講,賭場是最透明公開的場所。
如果不是這樣,進出賭場不知有多少亡命之徒,何鴻燊哪怕九條命都不夠,遑論活到98歲。
凱利公式不是憑空設想出來的,這個數學模型已經在華爾街得到了驗證,除了在賭場被奉為“勝利理論”,同時也被稱為“資金管理神器”,它是比爾格羅斯等投資大佬的心頭之愛,巴菲特依靠這個公式也賺了不少銀子。

回歸到賭場討論這個公式,根據f=(bp-q)/b公式結論,期望值(bp-q)為負時,賭徒不具備任何優勢,也不應下任何賭注。
賭 博這種遊戲,要下負賭注,你不如自己開個賭場當莊家。
世界上有為數不多的“賭神”,他們當中有資訊理論的發明者香農,數學家愛德華·索普等,他們通過一系列複雜的計算和艱深的數學理論,把某些賭戲的贏率扳回到50%以上,例如21點靠強大的心算能力可以把概率拉上去。
但就憑你讀書時上課打瞌睡、輸了只知道倍投翻本的可憐知識,以及九九乘法表的那點算力,還是先老實讀完以下3條準則。
①期望值(bp-q)為0時,賭局為公平遊戲,這時不應下任何賭注。
②期望值(bp-q)為負時,賭徒處於劣勢,更不應下任何賭注。
③期望值(bp-q)為正時,這時按照凱利公式投注賺錢最快,風險最小。
其實最終結論只有一個:除非100%贏,否則任何時候都別賭上全部身家,即使贏率相對較高也要謹慎。
十、贏得勝利的唯一法則:不賭
有人可能說,我又不是與何鴻燊對賭,我只要贏了對手就行了。
可無論是你還是對方,贏者都是要給賭場“流水”的,賭的時間一長,兩者都是在給賭場打工。
現代賭場自己做莊的可能性很小,他們更依賴數學定理來自己獲取利益。
賭王何鴻燊的數學到底怎麼樣,沒人知道。
只知他的兒子何猷君,從小就是數學天才,MIT史上最年輕金融碩士,連續兩年在“世界數學測試”邀請賽中獲獎。
沒有誰能說服一個墮落的賭徒,因為這是人格的缺陷。
但如果你還是一個具有理性精神的人,就別再迷戀所謂的運氣。
賭徒能夠依靠的是祖宗保佑,而賭場後面的大佬是高斯、凱利、伯努利這樣的數學大神。
你怎麼可能贏得了莊家?
論理性,沒有人能比賭場老闆更理性。
論數學,沒有人能比賭場老闆請的專家更精通數學。
論賭本,沒有人能比賭場老闆的本錢更多。
世上有太多人還在心存僥倖,告訴他唯一的答案。
如果要想真正贏得人生這場賭局,法則只有一個:不賭。
免責聲明:
本文觀點僅代表作者個人觀點,不構成本平台的投資建議,本平台不對文章信息準確性、完整性和及時性作出任何保證,亦不對因使用或信賴文章信息引發的任何損失承擔責任
相關閱讀

【好文】馬丁.舒華茲的交易原則大攻略
馬丁.舒華茲是華爾街頂尖短線炒手。從4萬美金起家,後來將資本變成了2000萬美元。

【好文】德州撲克對期貨股票交易的啟示:為什麼贏的人經常一直贏,輸的一直輸?
我有一個推測:牌齡一旦超過一星期的人,那他/她在最初打牌的時候手氣大概率是非常順的,而但凡成為了撲克圈一員的人,他/她必定體驗過所謂的“新手運氣”。

【好文】倒著想!頂尖投資大師的思考邏輯
反過來想,問題會變得更容易……

【好文】如果把交易比作游泳過河,你的游泳段位是什麼水準?
好久沒有寫點東西了,因為交易的信心沒有了。於是我決定放慢速度,把心態擺正。
天眼交易商
熱點資訊
英國FCA取消對KBFS Financial Limited的授權
塞浦路斯CYSEC對11家未經授權的投資公司發出警告
Bitcore最新受害者爆料詐騙手法:網友加LINE邀投資,誘導加碼拒出金
澳洲ASIC監管機構吊銷了JB Markets的澳洲金融服務牌照
交易環境測評:2024年外匯券商點差排行榜TOP5
爆雷跑路黑平台HERO竟有共犯?起底外匯跟單資金盤Gainer蓋諾
塞浦路斯CYSEC 將 Leverate利瑞從投資者補償基金中除名
FCA 警示可疑複製公司冒充合法的Forexeze Limited
外匯經紀商是怎麼賺錢的?他們和交易者是命運共同體嗎?
塞浦路斯CYSEC對FXORO母公司處以36萬歐元罰款
匯率計算


